What is Desmos?
Desmos is the built-in graphing calculator on the Digital SAT®. It lets you plot equations, inequalities, and functions quickly and interactively. Instead of solving every equation by hand, you can see the answer in the graph. Using it wisely can save you 30+ seconds per question. However, we recommend you first understand the concepts thoroughly solving problems by hand. For a more personalized SAT® prep approach, Sherpalai provides tailored strategies that complement these tools.
Quick Time-Saving Tricks
1. Find Intersections Fast:
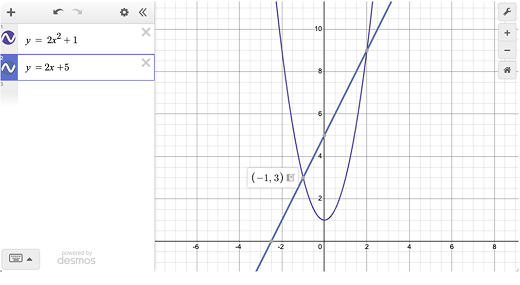
Example Question 1:
A line and a parabola are given by the equations y=2x+5 and y=2x²+1. At which points do the graphs intersect?
A. (-1,3) and (2,9) B. (-1,5) and (2,9) C. (-2,-1) and (3,11) D. (-1,3) and (3,11)
Solution:
Type y=2x+5 and y=2x²+1. Tap the intersection dot → Desmos shows (x,y). This gives option A as the right answer. Saves ~45–60 sec.
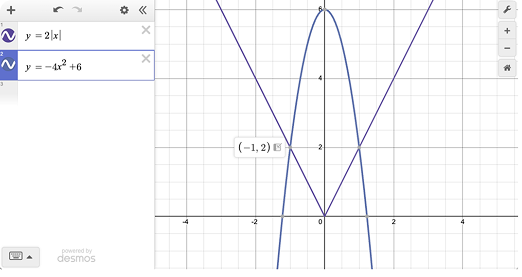
Example Question 2:
A company is designing a decorative archway in the shape of a parabola given by y=-4x²+6 and a support beam whose cross-section follows the function y = 2|x|. The points where the beam and the arch meet are attachment points for the structure. What is the slope of the line that passes through these two points of intersection?
A. 0 B. 0.5 C. 1 D. 2
Solution:
Type y=2|x| and y=-4x²+6. Tap the intersection dots: (-1,2) and (1,2). The line through these points is horizontal (same y-coordinate). Slope = (2-2)/(1-(-1)) = 0 which is option A.
2. Problems related to Inequalities and Shaded Regions:
Example Question:
A company is designing a region in the coordinate plane that satisfies two conditions:
- The point (x,y) lies above the line y=2x+1.
- The point (x,y) lies below the line y=-x+5.
Which of the following points lies in the shaded region that satisfies both conditions?
A. (0,0) B. (0.5,2) C. (0,3) D. (2,5)
Solution:
Graph y>2x+1 and y<–x+5. The overlap is shaded automatically. Only option C satisfies both conditions.

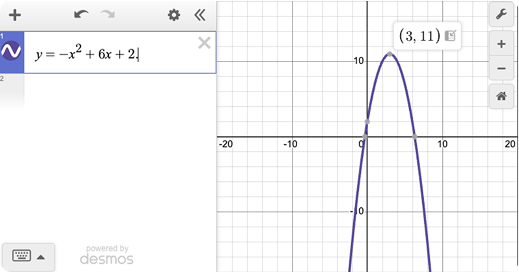
3. Questions based on finding Max / Min of functions:
Example Question:
What is the maximum value of the function f(x) = =–x²+6x+2.
Solution:
Graph y=–x²+6x+2. Tap the vertex → (3,11) is the max. The maximum value of f(x) is 11 which occurs at x = 3.
Tap points where y = 0 to get the roots. Saves ~30–45 sec.
4. Questions based on finding roots of a function:
Example Question:
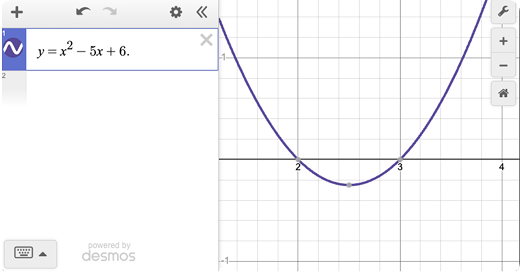
Determine the sum of the x-intercepts of the function f(x) = x²–5x+6.
Solution:
Graph y=x²–5x+6. Notice the roots (x-intercepts, i.e., y = 0) are at (2,0) and (3,0). The sum of x-intercepts is 2 +3 = 5.
5. Use Table for Quick Values:
Example Question:
A student’s experimental model is the line through the points (0,2) and (1,6). A theoretical model predicts y = x²+2x+3. For which x is the absolute error between the experimental and theoretical model minimal.
Solution:
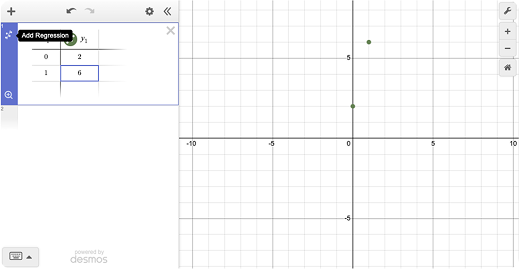
First, you need to determine the equation that models the experimental data. This is nothing but the line that passes through the points (0,2) and (1,6). To do it the Desmos way, add a table by clicking “+” 🡪 table and enter the points.

Then “Add Regression” to get equation of the line.
Then enter y = x²+2x+3 (theoretical model). Click on the intersection point (1,6) which gives the value of x where the error between the models is the least (i.e., 0 error in this case as the line and curve intersect).

6. Algebra word problems:
Example:
If the product of two positive integers is 16 and one integer is 2 more than three times of the second integer, what is the value of the larger integer?
Solution:
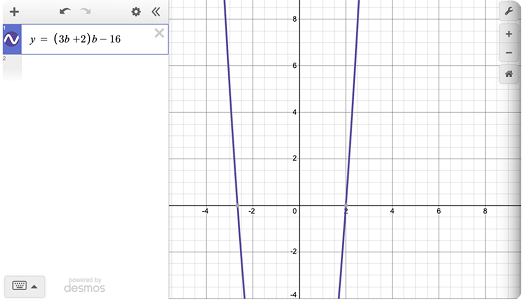
Convert the problem to an equation. Assume the second integer is b. The equation to enter is Desmos is y = (3b + 2)b - 16. Using Desmos, the positive x-intercept is b = 2. Therefore, the larger integer 3b+2 = 8.
7. Geometry problems to determine radius/center of a circle when the circle equation is given in the expanded form
Example Question:
What is the radius of a circle that is represented by the equation:
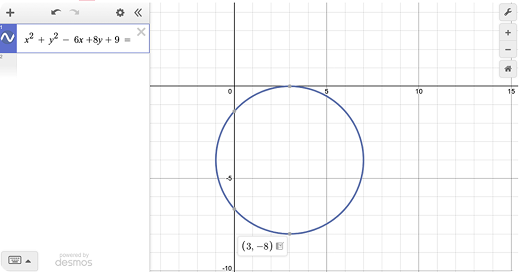
x² + y² - 6x + 8y + 9 = 0
Solution:
1. Enter x² + y²- 6x + 8y + 9 = 0. Click on the circle to reveal the min and max points.
2. Use “export point to expression list” for both points
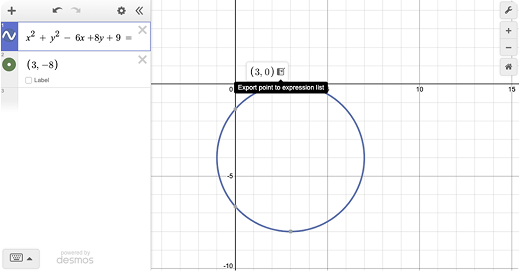
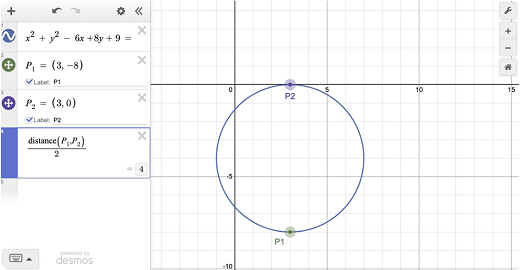
3. Label the points and use distance formula to get radius. The center of the circle is (3,-4) taking the average of P1 and P2.
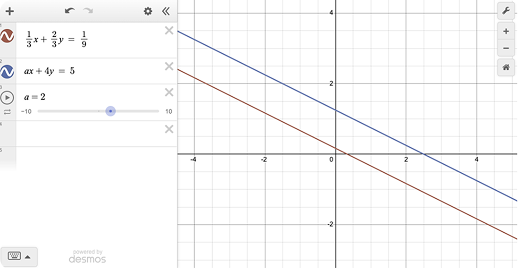
8. Using sliders for solving no solution/infinite solution problems
Example Question:
If the given system of equations has no solution, what is the value of a?
13x+23y=19
ax+4y=5
Solution:
Enter the equations as shown below. Slide a to find when the lines are parallel. Using Desmos may be helpful for MCQs where you can eliminate options. For FRQs, we suggest you solve such questions by hand to get an exact solution which may be hard to estimate with Desmos.